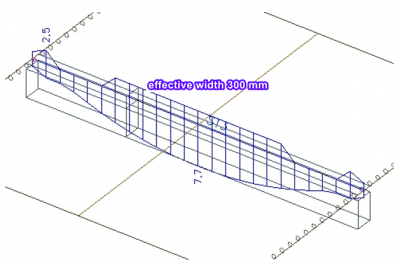
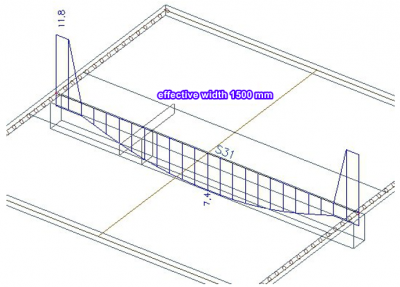
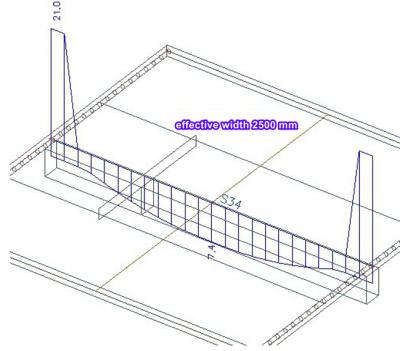
Osová síla v žebru
SCIA Engineer integruje žebra jako nosníky excentricky připojené k desce. Excentricita se spočte z poloviny tloušťky desky a poloviny výšky průřezu nosníku.
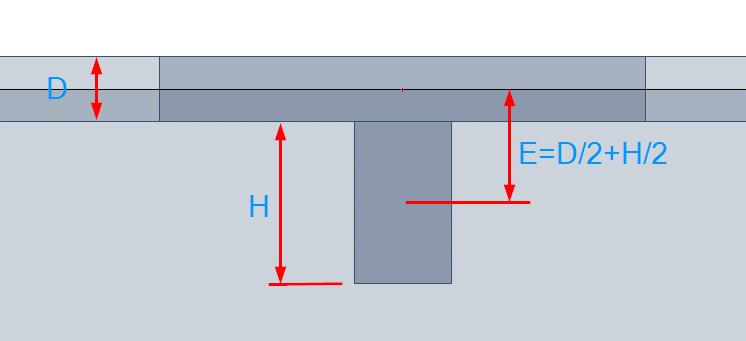
Při zadávání průřezu nosníku se výška průřezu definuje jako vzdálenost mezi spodní hranou desky a spodním okrajem nosníku. Na obrázku je výška označena jako „H“.
V důsledku posunu neutrální osy se vnitřní síly v celém systému mění. V jednoduchém systému zatíženém pouze ohybovým momentem získáme konstrukci s vnitřním ohybovým momentem i osovou silou.
Nosník je obvykle pod deskou a tak v desce vzniká tlak a v nosníku tah.
Excentricky připojený nosník způsobuje v desce osovou sílu. To pramení z deformace celého systému deska + nosník. Obrázek ukazuje vodorovnou deformaci „ux“, pomocí které chování systému ukážeme graficky. Systém se skládá ze dvou nosníků obdélníkového průřezu spojeného tuhými rameny. Podpora se může vodorovně volně pohybovat.
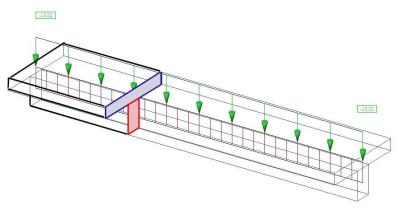
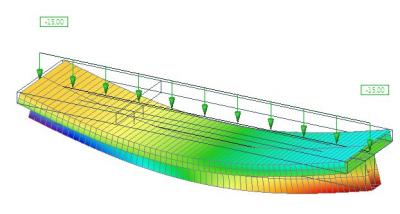
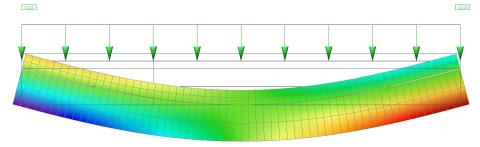
Vodorovná deformace v pohledu z boku:
Podíváme-li se na začátek nosníku, vidíme, že v desce vzniká tlak (červená šipka) a v nosníku tah (modrá šipka).
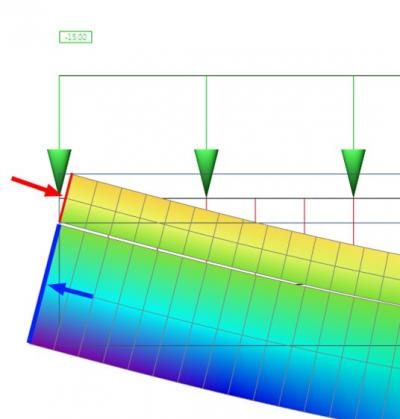
Celá soustava musí být v rovnováze a celková osová síla (součet osové síly v desce a osové síly v nosníku) musí být nulová.
V našem modelu máme pouze jeden nosník a všechny vnitřní síly z horní části jsou integrovány v osové síle žebra. V praxi to znamená, že spolupůsobící šířka desky je menší než celková šířka desky. Pouze výjimečně jsou žebra umístěna tak, že mezi spolupůsobícími šířkami není žádná mezera a všechny vnitřní síly v desce se sečtou do žebra. K tomu dojde, pokud je vzdálenost mezi žebry menší nebo rovna spolupůsobící šířce desky stanovené podle národní normy.
Chování žebra v široké desce
Nyní se můžeme podívat na systém, kde je šířka desky větší než spolupůsobící šířka žebra desky. Musí být splněna podmínka rovnováhy. Pokud zintegrujeme všechny osové síly v celé desce a v nosníku, dostaneme samozřejmě nulový výsledek.
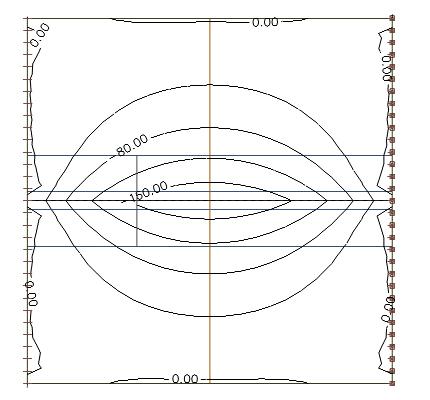
Podívejme se na rozložení osové síly na řezu vedeném středem desky:
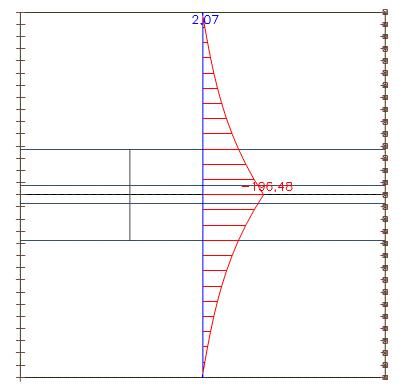
Osovou sílu na řezu můžeme integrovat po celé šířce desky. Dostaneme hodnotu 439 kN.
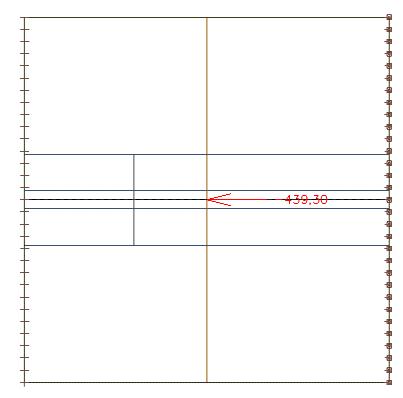
Tuto hodnotu můžeme porovnat s osovou silou v nosníku, která je 435 kN. Vidíme, že celá soustava je v rovnováze. Malý rozdíl vyplývá ze zvolené velikosti konečných prvků sítě.
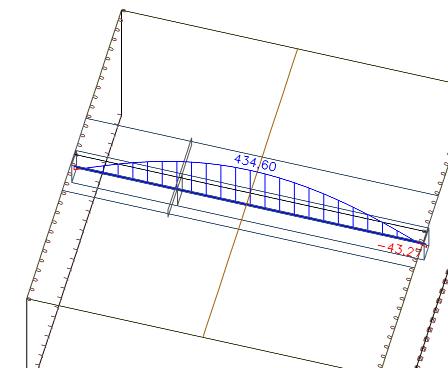
Porovnání různých spolupůsobících šířek
Pokud však zvětšíme spolupůsobící šířku žebra desky na celou šířku desky, zanedbáme průběh vnitřních sil v desce a koncentraci nad nosníkem. (Ve skutečnosti existují dvě limitní hodnoty: minimální spolupůsobící šířka rovná šířce nosníku a maximální spolupůsobící šířka rovná šířce celé desky.)
Vnitřní síly v desce jsou z desky vyjmuty a jsou integrovány do virtuálního T-průřezu. Tento virtuální průřez je složen ze spolupůsobící šířky desky a nosníku.
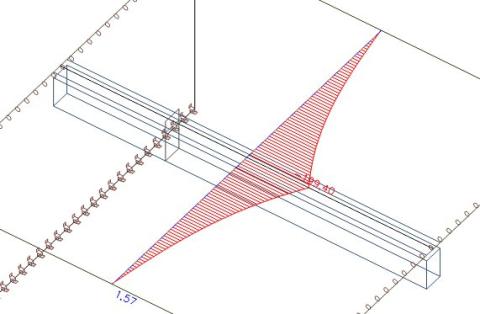
Průběh osové síly v desce. Vidíme, že průběh je shodný s výše uvedeným obrázkem, kde byla spolupůsobící šířka stanovena podle normy.
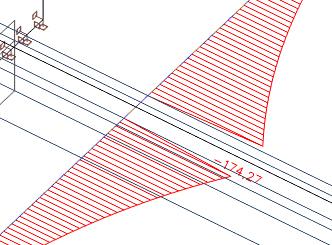
Na obrázku vidíme osovou sílu poté, co byla spolupůsobící šířka desky vyjmuta z desky. Ve SCIA Engineeru tohoto efektu dosáhneme zaškrtnutím volby „žebro“ v dialogu výsledků.
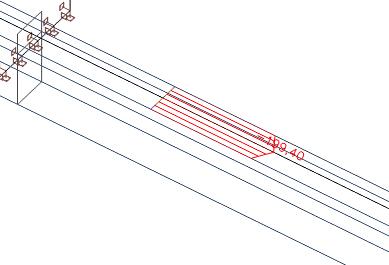
Osové síly uvnitř spolupůsobící šířky desky můžeme zintegrovat.
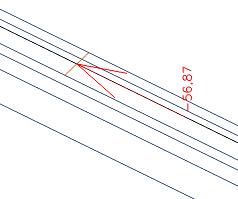
Dostaneme osovou sílu v desce rovnou 57 kN. Celková osová síla v desce je 435 kN. V části mimo spolupůsobící šířku proto máme osovou sílu 435 - 57 = 378 kN.
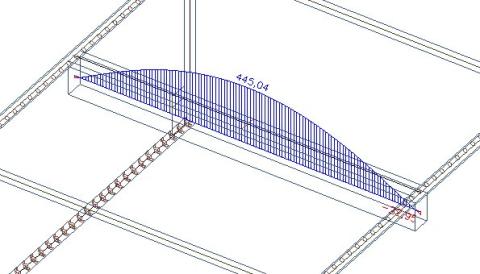
V nosníku máme stále 445 kN. (Rozdíl na předchozím obrázku pramení ze změny velikosti 2D konečných prvků).
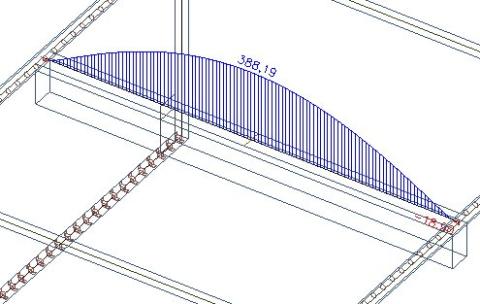
Pokud sečteme integrované osové síly v desce a v nosníku, musíme dostat 445 - 57 = 388 kN.
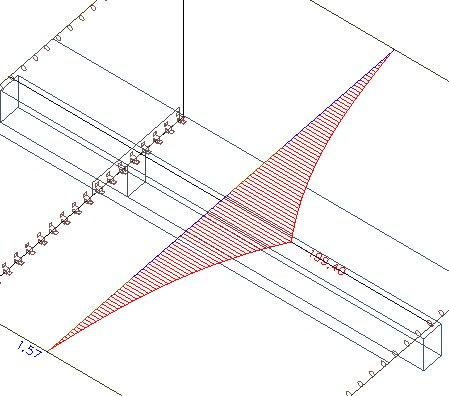
Podívejme se, k čemu dojde, pokud spolupůsobící šířku zvýšíme na 1 500 mm. Použijeme vzorec: 2 * (0,1 * L) + bw = 2*0,6+0,3.
Jak můžeme vidět, osová síla v desce je stále stejná. A také musí být, protože spolupůsobící šířka desky nemá na průběh vnitřních sil při výpočtu metodou konečných prvků žádný vliv. Vliv má pouze po výpočtu na rozdělení sil mezi desku a virtuální T-průřez.
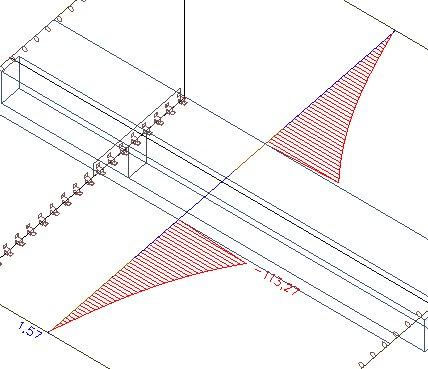
Plocha spolupůsobící šířky desky bude z desky odstraněna a sílu zintegrujeme do T-průřezu. Vnitřní síly mimo desku zůstanou v desce.
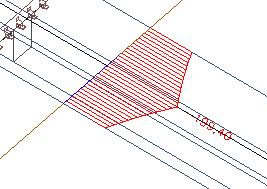
Tyto vnitřní síly budou přesunuty do T-průřezu.
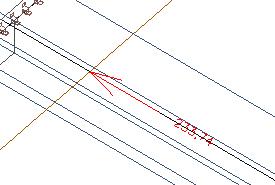
Pokud zintegrujeme osovou sílu, dostaneme 234 kN.
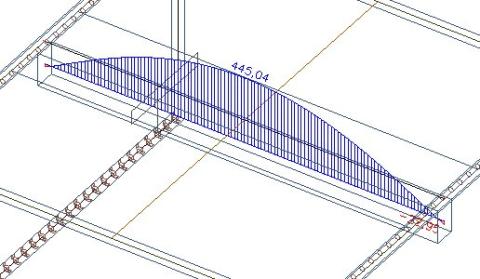
V obdélníkovém průřezu pod deskou dostaneme původních 445 kN.
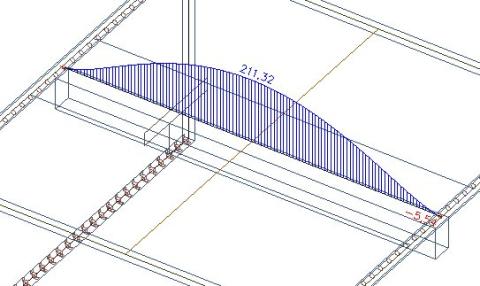
Pokud tuto osovou sílu v nosníku zmenšíme o 234 kN, což je součet osových sil od spolupůsobící šířky desky, zůstane 211 kN.
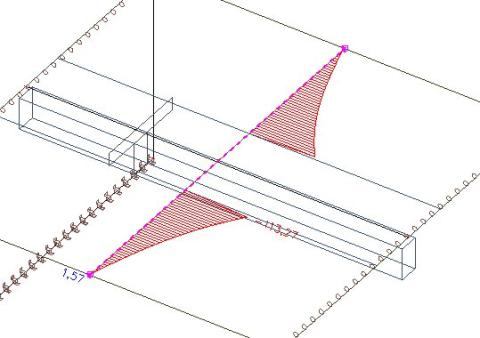
Osová síla mimo spolupůsobící šířku desky zůstane v desce.
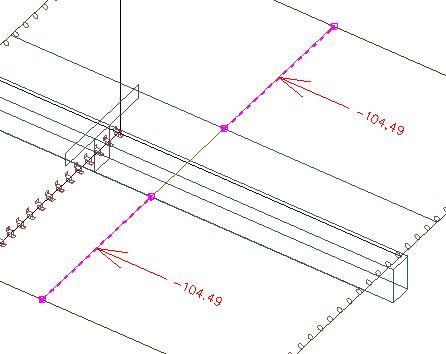
Pokud zintegrujeme síly (zleva doprava) mimo spolupůsobící šířku, dostaneme osovou sílu 210 kN, což je v rovnováze s tahem v žebru jakožto T-průřezem.
Závěr
Systém musí být v rovnováze. V našem jednoduchém systému složeném z desky a nosníku bez vodorovných sil musíme po integrování dostat nulové osové síly.
Vnitřní síly (v našem článku sledujeme pouze osovou sílu) budou rozloženy mezi desku a žebro. Tyto musí být v rovnováze.
Spolupůsobící šířka desky se použije pouze pro přepočet vnitřních sil (N, Vz, My, Mx) mezi desku a virtuální T-průřez. Na vnitřní síly v konečně-prvkovém modelu nemá žádný vliv.
Součet osových sil v celé desce musí být roven osové síle v obdélníkovém nosníku pod deskou. Pokud posuneme pouze část této osové síly uvnitř spolupůsobící šířky, některé části osových sil zůstanou jako tlak v desce mimo spolupůsobící šířku desky. (Buďme bez obav. Tyto síly budou uvažovány při návrhu výztuže desky.) A neuvažované osové síly zůstanou jako tah ve virtuálním T-průřezu žebra.
Existují však také jiné možnosti, jak modelovat žebro.
Můžeme definovat T-průřez bez excentricity. Při tomto způsobu modelování ovlivníme rozložení tuhosti mezi desku a nosník. Způsob definice spolupůsobící šířky desky má přímý vliv na tuhost systému a na vnitřní síly. Výhodou je, že v T-průřezu nevzniknou žádné osové síly, protože zde není žádná excentricita. Na druhou stranu, dostaneme lehce větší vlastní tíhu, protože tíha T-průřezu a desky se zdvojnásobí. Další nevýhodou je to, že máme výztuž v nosníku a v desce a musíme to uvést v dokumentaci.
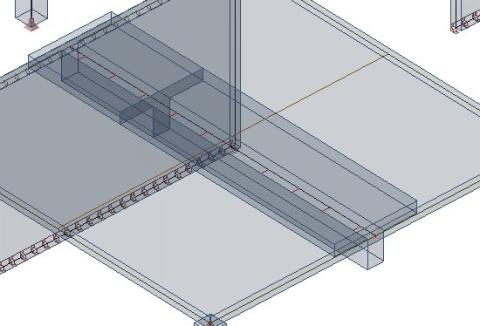
Další možností je definování náhradního obdélníkového průřezu. Princip je ten, že moment setrvačnosti systému deska + nosník se musí rovnat momentu setrvačnosti T-průřezu složeného z obdélníkového nosníku a spolupůsobící šířky desky. Odtud odvodíme výšku náhradního obdélníkového průřezu. (Více se dočtete v „Günter Rombach: Anwendung der Finite-Elemente-Methode im Betonbau).
Nyní můžeme porovnat spodní výztuž v žebru pro následující spolupůsobící šířky.
Porovnáme tři varianty, kde je: efektivní šířka rovna šířce nosníku tj. 300 mm, efektivní šířka 1500 mm stanovená dle EN 1992, náhodně zvolená hodnota efektivní šířky 2 500 mm.
Výslednou podélnou výztuž ovlivní také smyková síla, protože část smykové síly jde do třmínků, část do náhradní diagonály a část do podélné výztuže.