Highlights
- Spannkabel können als gerade oder durchhängend definiert werden. Bei durchhängenden Spannkabeln wird die anfängliche Kurvenform auf Grundlage des Eigengewichts des Spannkabels oder einer anderen, vom Benutzer eingegebenen verteilten Last berechnet.
- Zu den Eigenschaften des Spannkabels kann eine anfängliche Vorspannung hinzugefügt werden.
- Das Programm bietet eine geometrische nichtlineare Analyse für Spannkabel nach Newton-Raphson, die sich für Berechnungen mit großen Verschiebungen eignet.
- Berechnung von Schalenteilen als 2D-Elemente nur mit Axialzugsteifigkeit
- Nichtlinearitäten wie Nur-Zug- oder Nur-Druck-Teile oder nichtlineare Federn werden berücksichtigt.
- Die Ergebnisse enthalten Berechnungsbeulwerte (Verhältnis zwischen kritischer Beullast und angewendeter Last).
- Die verformte Form kann grafisch dargestellt werden.
- Der kritische Knickfall kann als anfängliche Verformung in die geometrische nichtlineare Berechnung importiert werden (in Verbindung mit dem Modul für geometrische Nichtlinearitäten).
Dieses Modul umfasst erweiterte Funktionalitäten für die geometrische nichtlineare Analyse, wie Spannkabel, Membranen und die sogenannte nichtlineare Stabilitätsanalyse.
Spannkabel
Ein Spannkabel ist ein Element mit nahezu keiner Biegesteifigkeit.
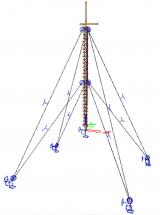
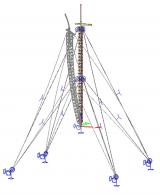
Zwei Spannkabelelemente können modelliert werden:
- gerade Spannkabel (vorgespanntes Element)
- durchhängende Spannkabel
Gerade Spannkabel
Für ein gerades Spannkabel muss lediglich die Vorspannungskraft eingegeben werden.
Hinweis: Dies setzt die richtigen Einstellungen auf der Registerkarte „Funktionalität“ im Dialog der Projekteinstellungen voraus. Die Optionen „Anfangsspannung“, „Nichtlinearität“, „Lokale Träger-Nichtlinearität“ und „Berechnung nach Theorie II. Ordnung“ müssen ausgewählt sein.
Durchhängende Spannkabel
Für durchhängende Spannkabel muss neben der Vorspannungskraft ein weiterer Parameter festgelegt werden. Das Spannkabel ist einer zusätzlichen Belastung ausgesetzt: entweder (i) der Belastung durch das Eigengewicht oder (ii) einer allgemeinen Last, die im gegebenen Winkel wirkt und wie die lokale Rotationsachse des 1D-Bauteils ausgerichtet ist. Mithilfe dieser Parameter wird der Durchhang des Spannkabels in einer bestimmten Richtung ermittelt. Alle Berechnungen werden an der „verformten“ Struktur ausgeführt. Die endgültige Verformung des Spannkabels wird also auf Grundlage des Durchhangs ermittelt, nicht auf Grundlage der idealen geraden Form des 1D-Bauteils.
Hinweis: Dies setzt die richtigen Einstellungen auf der Registerkarte „Funktionalität“ im Dialog der Projekteinstellungen voraus. Die Optionen „Anfangsspannung“, „Nichtlinearität“ und „Berechnung nach Theorie II. Ordnung“ müssen ausgewählt sein. Die Option „Lokale Träger-Nichtlinearität“ sollte nicht aktiviert werden, da dies die Berechnungsdauer unnötig verlängern würde.
Hinweis: Für diese Art der Analyse darf NUR das Newton-Raphson-Verfahren verwendet werden. Das Timoshenko-Verfahren darf für die Analyse durchhängender Spannkabel NICHT angewendet werden.
Beim Einfügen in das Modell wird ein 1D-Bauteil mit dieser Art Nichtlinearität durch ein entsprechendes Symbol gekennzeichnet. (Beachten Sie, dass das Symbol nur angezeigt wird, wenn die Anzeige der Modelldaten in den Anzeigeparametern aktiviert ist.)
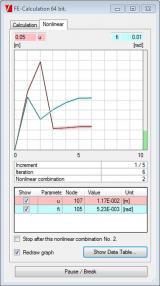
Technischer Hintergrund
Für diese Art der Analyse wird kein besonderes finites Element verwendet. Es wird ein normales 1D-Bauteilelement verwendet, dessen Biegesteifigkeit jedoch sehr klein ist. Geringe Querkräfte, die während der iterativen Berechnung auftreten, werden ignoriert.
Membrane
Dieses Modul ermöglicht die Verwendung von Membranelementen. Membranelemente sind Schalenelemente, die keine Biegesteifigkeit und keine Axialdrucksteifigkeit aufweisen. Daher können Membranelemente zur Modellierung von Planen, Netzen usw. verwendet werden, die zentrischem Zug ausgesetzt sind.
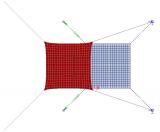
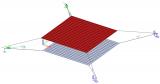
Um realitätsnahe Ergebnisse zu erhalten, muss eine Berechnung nach Theorie II. Ordnung mit der Newton-Raphson-Verfahren ausgeführt werden.
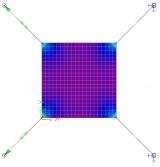
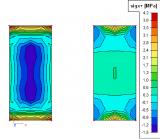
Unterschiede bei den Ergebnissen für Membranelemente und für Standardelemente
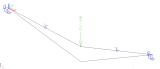
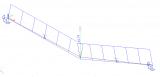
Das Anwenden des Membranelementverhaltens führt zu anderen Ergebnissen als für Standardelemente. Dies lässt sich am einfachsten an einem Beispiel veranschaulichen. Gehen Sie von einer rechteckigen Platte aus, die aus einem sehr dünnen Stahlblech gefertigt ist. Die linke Abbildung zeigt die Ergebnisse für ein standardmäßiges 2D-Bauteil. Die rechte Abbildung zeigt die Ergebnisse für ein Membranelement.

Hinweis: Membranelemente können nur in einer allgemeinen XYZ-Umgebung modelliert werden. Weil die Biegesteifigkeit null ist, können keine Rippen, keine vorgespannten Spannglieder, keine orthotropen Parameter und keine physikalischen nichtlinearen Daten an einem Membranelement eingegeben werden. Da ein Membranelement keine Axialdrucksteifigkeit aufweist, können an dieser Art Element keine Betonberechnung und keine Berechnung der normabhängigen Verformung ausgeführt werden.
Nichtlineare Stabilitätsanalyse
Stabilitätsberechnungen geben Einblick in die Knickmechanismen einer Struktur, dienen der Berechnung der Knicklänge eines Bauteils für den Stahlnachweis und beispielsweise der Überprüfung, ob Berechnungen nach Theorie II. Ordnung erforderlich sind.
Mit diesem Modul können Sie den globalen kritischen Knickfall und die Beullast von Rahmenstrukturen unter Berücksichtigung nichtlinearer Wirkungen ermitteln. Die Berechnung erfolgt in zwei Stufen. In der ersten Stufe wird die Last inkrementell erhöht, bis die Struktur instabil wird. Die Berechnungen berücksichtigen dabei nichtlineare Effekte. In der zweiten Stufe werden der Knickfall und die Beullasten ermittelt.
Wenn die Beullast bekannt ist, können Sie für jede Struktur festlegen, ob eine Berechnung nach Theorie II. Ordnung erforderlich ist. Die Bauvorschriften geben die Höchstwerte für Belastung und Knickfälle an, für die Berechnungen erster Ordnung ausgeführt werden.
Vom globalen Knickfall der Struktur können Sie die kritische anfängliche Verformung für eine Berechnung nach Theorie II. Ordnung ableiten.
Erforderliche Module:
- sens.00

SCIA ENGINEER selbst ausprobieren?
Entdecken Sie, wie unsere Software und Dienstleistungen Ihnen helfen können, Ihre Arbeit zu optimieren und Ihre Produktivität zu steigern. Probieren Sie es selbst mit einer 30-Tage-Test.
Laden Sie eine kostenlose 30-Tage-Testversion herunter
Fordern Sie ein Vorführung über SCIA Engineer an
Kontaktieren Sie den Support für weitere technische Informationen