Belangrijkste kenmerken
- De kabel kan worden gedefinieerd als recht of slap. Voor slappe kabels wordt de oorspronkelijke kromming berekend voor het eigengewicht van de kabel of voor een andere, door de gebruiker ingevoerde verdeelde belasting.
- Initiële voorspanning kan aan de kabeleigenschappen worden toegevoegd.
- De geometrische niet-lineaire analyse van kabels maakt gebruik van de Newton-Raphson-methode die geschikt is voor het berekenen van grote verplaatsingen.
- Berekening van schalen als 2D-elementen met alleen axiale trekstijfheid.
- Er wordt rekening gehouden met niet-lineariteiten, zoals elementen met alleen spanning/druk, niet-lineaire veren en dergelijke.
- De resultaten omvatten berekende knikfactoren (verhouding tussen de kritieke knikbelasting en de toegepaste belasting).
- Vervormingen kunnen grafisch worden weergegeven.
- De kritieke knikmodus kan worden geïmporteerd in de geometrische niet-lineaire berekening als een oorspronkelijke vervorming (in combinatie met de geometrische niet-lineaire module).
Deze module bevat geavanceerde functies voor geometrische niet-lineaire analyse van bijvoorbeeld kabels, membranen en zogenaamde niet-lineaire stabiliteitsanalyse.
Kabels
Een kabelelement is een element met nagenoeg geen buigstijfheid.
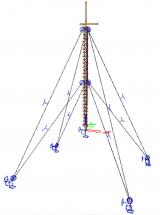
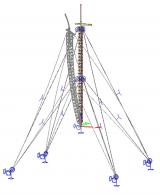
Twee kabelelementen kunnen worden gemodelleerd:
- rechte kabel (voorgespannen element)
- slappe kabel
Rechte kabels
Voor een rechte kabel wordt alleen de voorgespannen kracht ingevoerd.
Opmerking: De correcte instellingen moeten worden uitgevoerd in het dialoogvenster Projectinstellingen, tabblad Functionaliteit. De opties Initiële spanning, Niet-lineariteit, Staaf lokale niet-lineariteit en 2de-ordeberekening moeten worden geselecteerd.
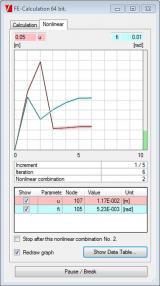
Slappe kabels
Behalve de voorgespannen kracht moeten voor een slappe kabel een extra parameter worden ingesteld. De kabel is onderworpen aan extra belasting: ofwel (i) belasting door eigen gewicht, ofwel (ii) een algemene belasting die werkzaam is onder een bepaalde hoek met dezelfde richting als de fixatie van de lokale rotatieas van het 1D-element. Met deze parameters wordt de slapheid van de kabel in een bepaalde richting bepaald. Alle berekeningen worden uitgevoerd op de "vervormde" structuur. Dit betekent dat de uiteindelijke vervorming van een kabel wordt berekend op grond van deze "slappe" vorm en niet op grond van de ideale rechte vorm van het 1D-element.
Opmerking: de correcte instellingen moeten worden uitgevoerd in het dialoogvenster Projectinstellingen, tabblad Functionaliteit. De opties Initiële spanning, Niet-lineariteit en 2de-ordeberekening moeten worden geselecteerd. De optie Staaf lokale niet-lineariteit hoeft niet te worden ingeschakeld omdat de berekening anders onnodig veel tijd kost.
Opmerking: UITSLUITEND de Newton-Raphson-methode kan voor dit soort analyses worden ingezet. De Timoshenko-methode MAG NIET worden uitgevoerd voor het analyseren van slappe kabels.
Als een 1D-element met dit type niet-lineariteit in het model wordt ingevoegd, wordt dit gemarkeerd met een eigen symbool (om het symbool te kunnen zien, moeten de weergaveparameters worden aangepast om modelgegevens weer te geven).
Technische achtergrond
Voor dit soort analyses wordt geen speciaal eindig element gebruikt. Er wordt een regulier 1D-element gebruikt, maar de buigstijfheid ervan is uitermate klein. Kleine afschuifkrachten die tijdens de iteratieve berekening verschijnen, worden verwijderd.
Membranen
Deze module maakt het mogelijk om membraanelementen te gebruiken. Membraanelementen worden gedefinieerd als schaalelementen zonder buigstijfheid en axiale drukstijfheid. Daardoor kunnen membraanelementen worden gebruikt voor het modelleren van bijvoorbeeld canvas en netten die zijn blootgesteld aan axiale trek.
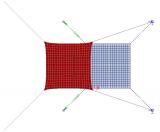
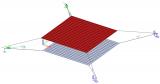
Voor het verkrijgen van realistische resultaten moet een 2de-ordeberekening worden uitgevoerd waarbij de Newton-Raphson-methode wordt gebruikt.
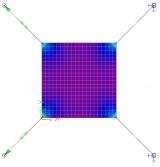
Verschillen in de resultaten tussen membraan- en standaardelementen
Het verschil in de verkregen resultaten als gevolg van het toepassen van het membraangedrag kan het beste worden gedemonstreerd aan de hand van een eenvoudig voorbeeld. We gaan uit van een rechthoekige plaat die is gemaakt van een zeer dun staal. Links in de figuur ziet u de resultaten die zijn verkregen voor een standaard 2D-element. Rechts ziet u de resultaten voor de membraanelementen.

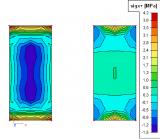
Opmerking: membraanelementen kunnen alleen worden gemodelleerd in een algemene XYZ-omgeving. Doordat de buigrigiditeit nul is, kunnen voor een membraanelement geen ribben, voorgespannen spanelementen, orthotropische parameters of fysische niet-lineaire gegevens worden ingevoerd. Aangezien een membraanelement geen axiale drukstijfheid heeft, kan er voor dit type element geen betonberekening of NAV worden uitgevoerd.
Niet-lineaire stabiliteitsanalyse
Stabiliteitsberekeningen worden gebruikt om inzicht te krijgen in de knikmechanismen van een structuur, om de kniklengte van een element te berekenen om in de staalnormcontrole te gebruiken, om te controleren of tweede-ordeberekeningen nodig zijn, enzovoort.
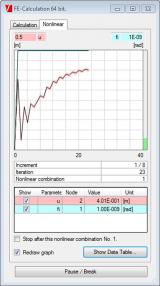
Deze module helpt bij het bepalen van de algemene kritieke knikmodus en de knikbelasting van raamwerkstructuren terwijl rekening wordt gehouden met niet-lineaire effecten. De berekening wordt uitgevoerd in twee fasen. De eerste fase verhoogt de belasting stapsgewijs totdat de structuur instabiel wordt, waarbij rekening wordt gehouden met niet-lineaire effecten. De tweede fase bepaalt de knikmodus en knikbelasting.
Als de knikbelasting bekend is, kunt u voor elke constructie bepalen of een tweede-ordeberekening nodig is. De bouwcodes leveren de limieten voor het gebruik van eerste-ordeberekeningen wat belasting en knikbelasting betreft.
U kunt voor een tweede-ordeberekening de kritieke oorspronkelijke vervorming afleiden uit de algemene knikmodus van de constructie.
Vereiste modules:
- sens.00
