Veelvoorkomende oorzaken van instabiliteiten
De FAQ Waarschuwing: stijfheidsmatrix is enkelvoudig, constructie is instabiel legt uit hoe je de aangeduide (net)knopen kan vinden.
Deze FAQ legt een aantal vaak voorkomende oorzaken van instabiliteiten uit.
SCHARNIEREN EN VERBINDINGEN
In de meeste gevallen worden instabiliteiten veroorzaakt door fouten in het modelleren van de verbindingen tussen elementen of in de definitie van scharnieren.
Een veelvuldig gemaakte fout is het toelaten van alle rotatie-vrijheidsgraden om het buigend moment te elimineren uit de elementen, zoals getoond in volgende figuur:
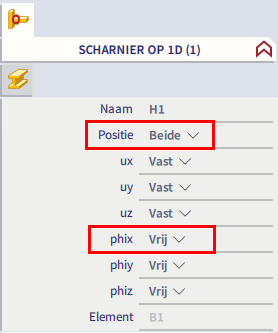
Deze instelling zorgt ervoor dat het element kan roteren om zijn eigen as, wat tot een instabiliteit leidt. De rotatie-vrijheidsgraad om de x-as mag nooit vrijgemaakt worden aan beide uiteinden van hetzelfde element.
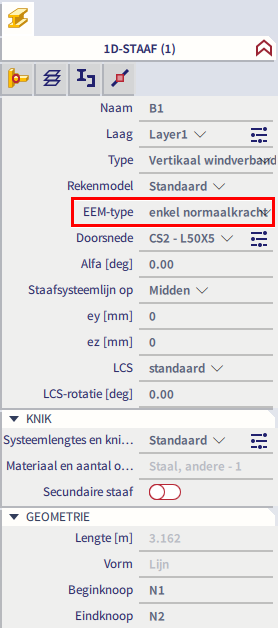
Bovendien is een elegantere en efficiëntere manier om het buigend moment te elimineren om geen scharnieren toe te passen, maar het element te definiëren als ‘enkel normaalkracht’, zoals in onderstaande figuur.
OPPERVLAKTE ONDERSTEUNING
Een andere bron van instabiliteiten komt voor bij het gebruik van een oppervlakte ondersteuning waarbij geen stijfheid wordt gedefinieerd in de horizontale richting:
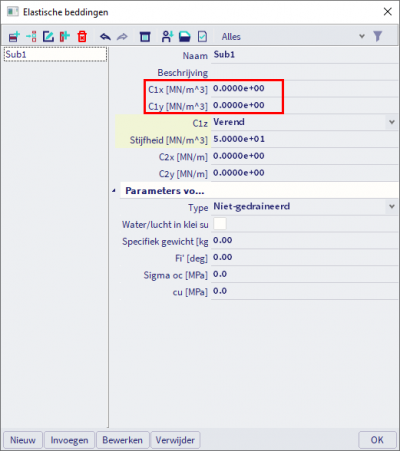
Tenzij de structuur via bijkomende steunpunten wordt verhinderd van zich horizontaal te verplaatsen, mogen de waarden voor C1x en C1y nooit ingesteld zijn als nul, aangezien in dat geval de structuur zich vrij in de horizontale richting kan verplaatsen, wat dus leidt tot een instabiliteit.
INSTABILITEIT TIJDENS NIET-LINEARE ANALYSE
Wanneer de lineaire berekening vlot wordt uitgevoerd, maar de niet-lineaire berekening stopt omwille van een instabiliteit, kan het zijn dat de structuur niet in staat is de opgelegde belastingen te dragen. De niet-lineaire solver kan enkel een oplossing vinden wanneer de structuur stabiel is: wanneer de structuur instabiel wordt (knik), stopt de niet-lineaire berekening. In deze gevallen zal je het ontwerp van de structuur moeten herevalueren/aanpassen zodat deze de opgelegde belasting toch kan dragen.
Om te bevestigen dat je in dit geval zit, kan je een (lineaire) stabiliteitsanalyse uitvoeren om de laagste alpha kritiek waarde te controleren: als deze waarde lager is of bijna gelijk is aan 1, betekent dit dat de structuur de belasting bij de niet-lineaire analyse niet zal kunnen dragen.