Modélisation d'un élément "traction seule"
Suivez les étapes décrites ci-dessous pour modéliser un élément « tension uniquement » (vous avez besoin du module de base sens.00 Basic nonlinear calculation pour cela).
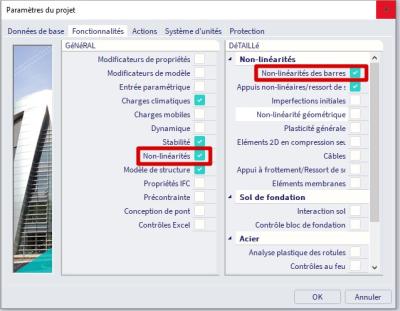
1) Dans la boîte de dialogue Données du projet (menu principal > Fichier > Paramètres du projet), dans l’onglet 'Fonctionnalité', les fonctionnalités 'Nonlinéarité' et 'Non-linéarité locale du faisceau' doivent être sélectionnées:
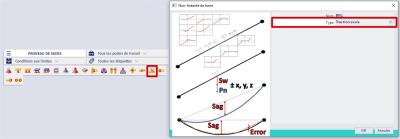
2) Dans le panneau de saisie > structure du poste de travail > catégorie Conditions aux limites (ou via le SCIA Spotlight), un nouvel élément 'Nonlinearity1D' est maintenant disponible:
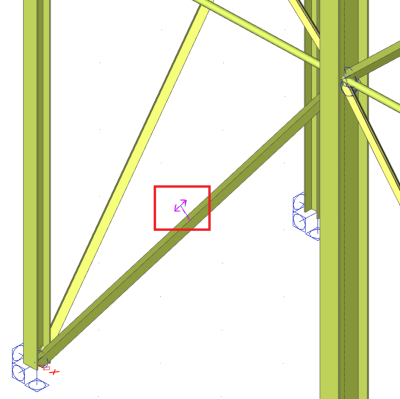
Choisissez « Tension uniquement » et sélectionnez les barres qui ne doivent fonctionner que sous tension et non sous compression. Les étiquettes apparaîtront sur les barres sélectionnées, sous forme de flèches.
3) L’étape suivante consiste à créer des combinaisons non linéaires via le menu principal > Bibliothèques > Cas de chargement, combinaisons > Combinaisons non linéaires.
Pour plus d’informations, reportez-vous à la FAQ Combinaisons non linéaires.
4) Maintenant, l’analyse non linéaire peut être effectuée. Il s’agit d’un calcul itératif, au cours duquel la compression sera éliminée des barres de « tension uniquement ».
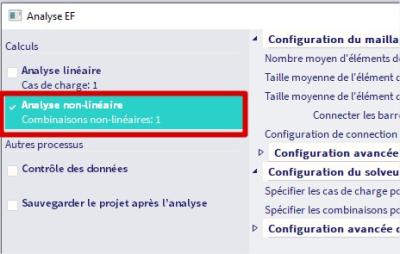
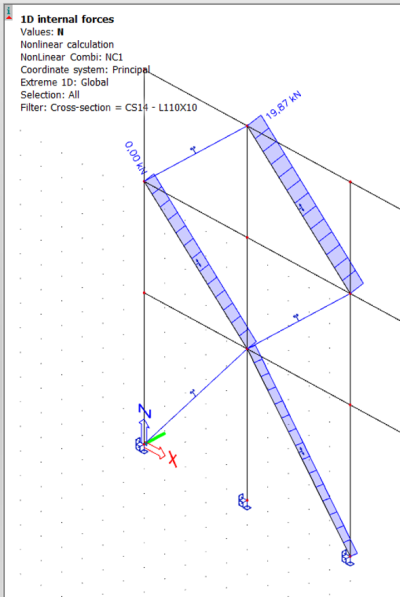
5) Les résultats pour la force normale - dans une sélection de barres de « tension uniquement » - peuvent maintenant être visualisés et comparés via le menu principal > Résultats > membres 1D > Forces internes.
- Résultat pour une combinaison linéaire :
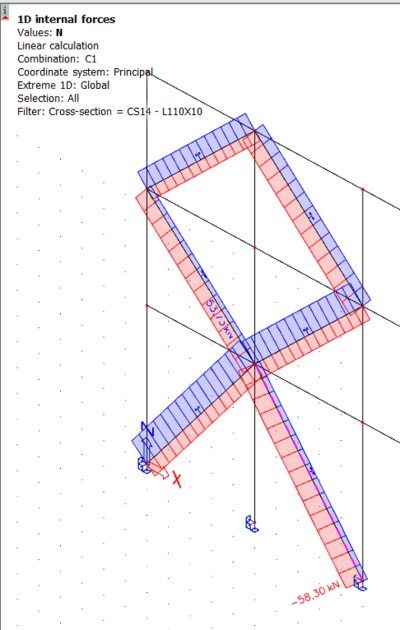
- Résultat pour une combinaison non linéaire (avec le même contenu de charge que la combinaison linéaire) :