Highlights
- Second order calculations
- Local and global imperfections
- Large deformations
- P-delta effect
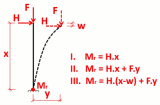
This module allows you to perform second order calculations. These allow the calculation of the structure in its deformed condition, taking into account the P-Delta effect (initial displacements and element imperfections), as well as the influence of normal forces on the stiffness.
A second order analysis can be performed on an initially deformed structure taking into account geometric imperfections (initial deformations and element imperfections):
- Local curvature imperfection specified by user or according to Eurocode
- Overall imperfection specified by the user or in accordance with Eurocode
- General buckling shape from stability analysis
1st Order Analysis
This is the standard linear calculation. It may be used only when the displacement effects on the structural behaviour are negligible.
2nd Order Analysis: Timoshenko method
This method is based on the exact Timoshenko solution for members with known normal force. It is a 2nd order theory with equilibrium on the deformed structure which assumes small displacements, small rotations, and small strains. The influence of the normal force on the bending stiffness and the additional moments caused by the lateral displacements of the structure (the P-Δ effect) are taken into account in this method. The method needs only two iteration steps, which leads to a great efficiency. In the first step, the axial forces are solved. In the second step, the determined axial forces are used for Timoshenko’s exact solution. As default iteration method is set Picard method. This is suitable for most cases of nonlinear behaviour of buildings, and it is set as default for geometrical nonlinearity

2rd Order Analysis: Newton Raphson method
It is also called “large deformations” analysis and is based on the Newton-Raphson method for the solution of non-linear equations. This method is a more general applicable method which is very solid for most types of problems. It can be used for very large deformations and rotations; however, it is also suitable for small displacements and small strains. Mathematically, the method is based on a step-by-step augmentation of the load. This type of iterative solution is suitable mostly for models with membranes and cables like for example bridges.

