Experimental and numerical comparative analysis of a SFRC slab on piles
Lukáš Dlouhý, Product Development Engineer, SCIA, Brno, Czech Republic
Rémy Roland, Technical Manager South Europe & Africa, Bekaert, Zwevegem, Belgium
FRC2018: Fibre Reinforced Concrete: from Design to Structural Applications
Joint ACI-fib-RILEM International Workshop


Abstract
In order to investigate the behaviour of SFRC slabs on piles, a campaign of tests has been conducted at the Tongji University of Shanghai, China. All the specimen are reinforced with the 5D 65/60BG high performance fibre from Bekaert, at dosages of 30 and 35 kg/m³. Tests were conducted on four plates of dimensions 4.3x4.3m, with a thickness of 18cm, loaded by one central point and supported on four 4 points.
To gain a fundamental understanding of the structural behaviour, we have built non-linear FEM models using the SCIA Engineer 17 software, which has a built-in module for SFRC structures. Numerical simulation results are compared to experimental performance in terms of ultimate load and crack pattern.
Keywords
Steel Fibre Reinforced Concrete, Slab on piles, Finite Element Modelling
1 Introduction
As the steel reinforced fibre concrete is very often used mainly for foundation the real behaviour and investigation of a structure such as a slab on piles is essential. In this scope, this study aims to predict the ultimate capacity of the SFRC slab on piles of the Nanhui project in Shanghai.
This design has been done both by testing and by using a finite element model using SCIA Engineer.
Concerning the test campaign:
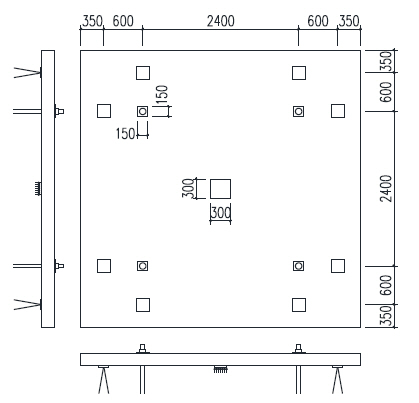
The projected structure is a square slab on piles with dimensions 14x14m supported on 49 piles having a central spacing of 3m and a peripheral spacing of 2m. This is of course too big to be tested in a laboratory so in a first step we will derive a suitable testing model with a size reduced to 4.3x4.3m. Then we describe the test setup and give the results.
Concerning the finite element model:
The model is made of plate elements with dimensions close to 5cm. Due to the symmetry of the test specimen only one quarter of the slab was modelled (i.e. 2.15x2.15m). The nonlinear calculation uses a very efficient damage material model called the Mazars model.
2 Experimental program
2.1 Specimen geometry
The geometry of the Nanhui project is the following:
Main design parameters:
- side span: l0=2m
- middle span: l1=3m
- slab thickness: h=187.5mm
- square pile size: 300mm×300mm
- concentrated load per span: 100 kN
In a first step, we did a complete finite element model of the slab to see the distribution of the bending moments. This is a linear model made with plate elements. The map of the bending moments is as follow:

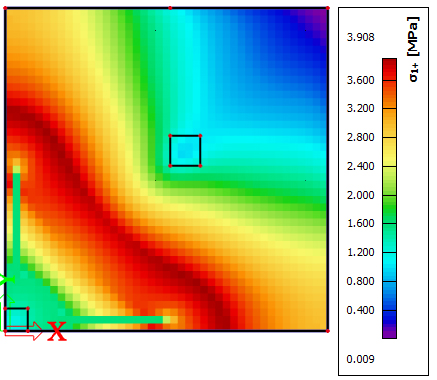
It can be seen 1.2 that the maximum moment is 22290N ·m, and the minimum moment value is -27090N ·m. The the bending moment on top of the pile is very close to the moment value at the middle of each span.
Now we look for a simplified structure with one central hydraulic ram and four bearings at the corners, the rotation of the model’s edge will be constrained to simulate the behaviour of the full plate. We can look at this model from two different point of view. On one hand we can see the ram as the pile and the bearings as the concentrated load (the model is centred on a pile). But we can also see the ram as the concentrated load and the bearings as the piles (the model is centred on the concentrated load).
We have found the structure depicted in the picture at the right as giving the same moments as the full structure.
The bending moment map of the test structure is the following:

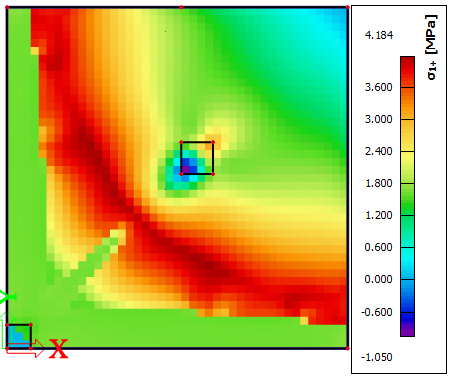
It can be seen that the maximum bending moment of the test model scheme is 26560 N ·m, compared with the bending moment of the prototype multi-span continuous pile bearing steel fibre reinforced concrete slab.
The error is as follows: (27090 - 26560) / 27090 = 1.96%
The test setup can be seen on the picture on the right where the slab’s dimensions are. 4300×4300×188 mm
During the test, the displacement and force of the central jack are recorded. In addition the displacement and strain of the top surface is recorded through the ARAMIS® system.
In the present investigation we have tested four square SFRC slabs.
2.2 Material properties
The concrete is a C40/50 and the post-crack flexural tensile strength have been measured according to EN 14651 for two dosages 30 kg/m³ and 35kg/m³ on 6 beams for each dosage.
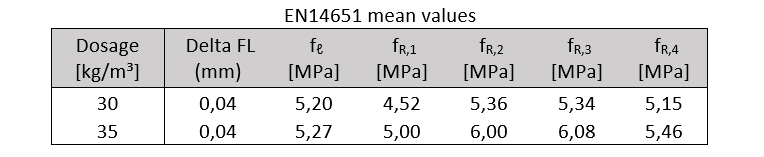
2.3 Test results
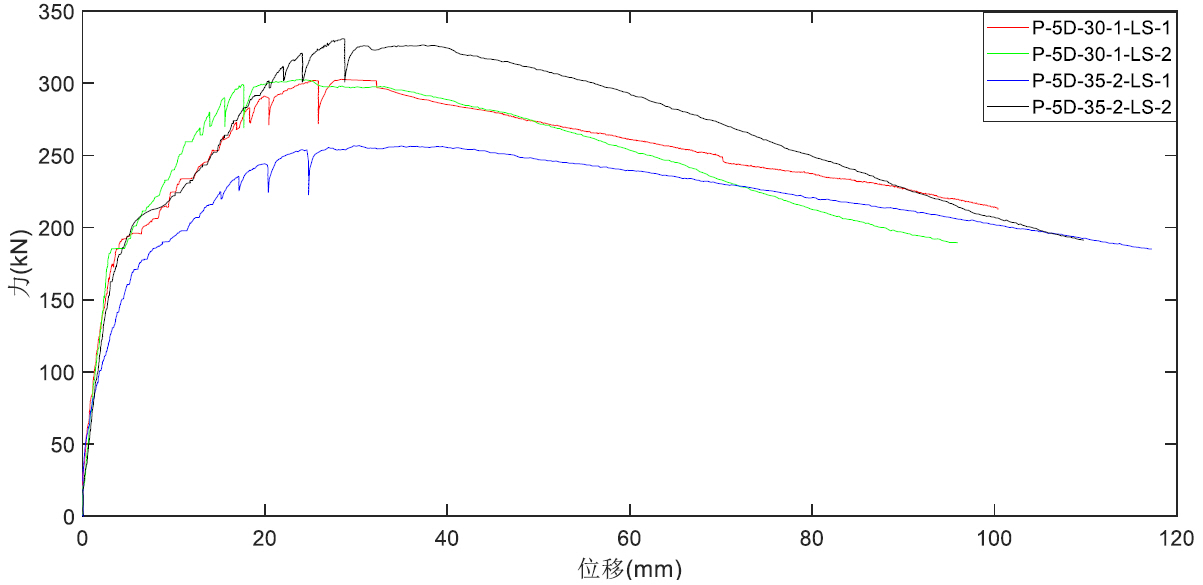
The force/displacement curves show an extended ductility far beyond the ultimate limit state, up to a deflection of 10cm.
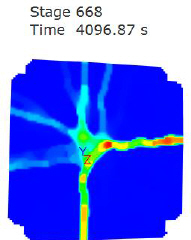
Crack patterns:
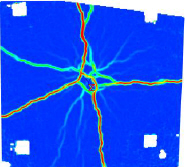

P-5D-30-LS-1: 1st crack force 302.7 kN
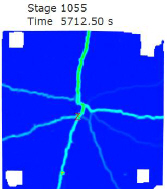
P-5D-30-LS-2: 1st crack force 302.5kN
P-5D-35-LS-1: 1st crack force 256.8kN
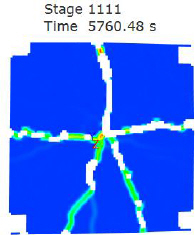
P-5D-35-LS-2: Cracking force 330.8kN
3 Nonlinear analysis in SCIA Engineer
3.1 Introduction
Physical non-linear analysis represents a very powerful tool for analysing any kind of structure in civil engineering created not only from steel fibre reinforced concrete but also from other materials. This type of analysis provides a stress distribution and increase of the bearing capacity after reaching the ultimate strain until the collapse mechanism. This mechanism is based on different values of stress and strain, dependent on a predefined nonlinear stress-strain relationship in the material diagram.
Currently there is no general part in EuroCode 2 for buildings regarding steel fibre concrete. There exist only recommendations as RILEM, Model code 2010 and mainly the German guideline DAfStb which was used as a basis for the numerical analysis outlined in this paper. Some papers have already been published regarding the verification of tests by FEM analysis, but using different approaches. The experimental test was simulated using numerical analysis in computational software SCIA Engineer, the structure consists of 2D plate elements.
3.2 Nonlinear material behaviour
Due to the symmetry of the test specimen only one quarter of the slab was modelled. Thanks to this fact it was possible to obtain precise results due to using a higher mesh density for the 2D elements. The dimension of the slab within the model was 2.15x2.15m. The load was imposed by a surface load presenting the real behaviour of the test. The mesh size was defined as 0,05m.
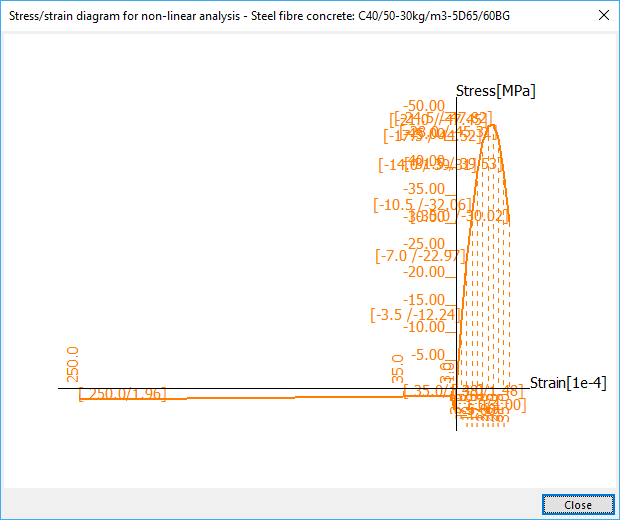
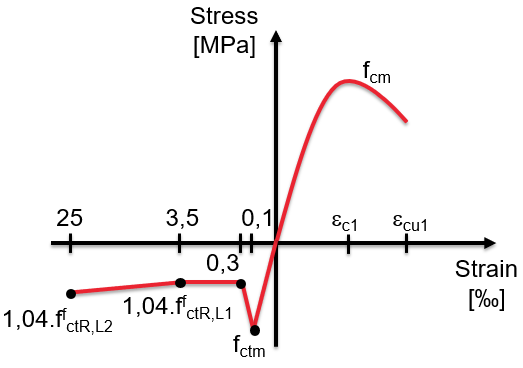
A typical shape of the stress-strain diagram is visible on the following figure, where a parabolic behaviour is used in compression in the same way as in standard concrete. The tensile behaviour displays a narrow peak expressed by the mean tensile strength. From the point of strain, this peak works very well as a crack localizator. After the crack formation, the toughness of steel reinforced fibre concrete allows to keep a certain level of tensile stress with increasing of the strain up to failure which is fixed at 25‰. Generally, there are two types of tensile branches based on the selected fibre type, with softening or hardening post-cracking behaviour (DRAMIX 5D with an ascending branch and 3D/4D with a descending branch in tension). The diagram for nonlinear analysis is prepared based on a user defined dosage and the points are generated according to the requirements in the DAfStb Guideline "Steel fibre reinforced concrete», figure R.1.
3.3 Mazarz material damage model
The nonlinear calculation uses a very efficient damage material model called the Mazars model. This material model is very well applicable for a material diagram with peaks and descending stress-strain diagrams typical for steel fibre concrete. The combination of elasticity and damage behaviour is combined in this material model. Moreover, the damage description is considered as isotropic and directly affecting the stiffness matrix. The so called “effective damage parameter” determines changes of the stiffness depending on the loading. Additionally, the effect of cracks must be considered during application. Here an analogy with the thermodynamic variable is applied for the two main damage states which are cracking of concrete in tension and crushing in compression. In case of plotting the surface failure of the steel fibre reinforced concrete the very well-known curve described by Kupfer for biaxial loading is obtained which is also typical for regular reinforced concrete.
3.4 Results
The presented nonlinear model provides good match with the experimental test. The comparison of the results with the load-displacement diagram coming from the test is visible on figure [Fig. 5] for Dramix fibres 5D65/60BG with dosage 30kg/m3 and 35kg/m3. This capacity is at the load level 283,9kN (299,0kN for 35kg/m3 respectively) where the ultimate tensile strain in steel fibre reinforced concrete (25‰) is reached. In fact graphs Calc-30 correspond to P-5D-30-1-LS-1 and Calc-35 to P-5D-35-1-LS-2.
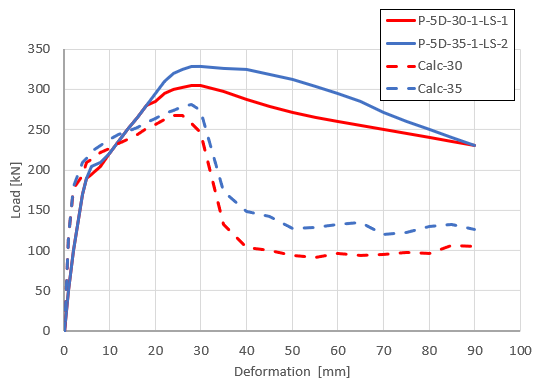
Figure 5 – Load displacement distribution
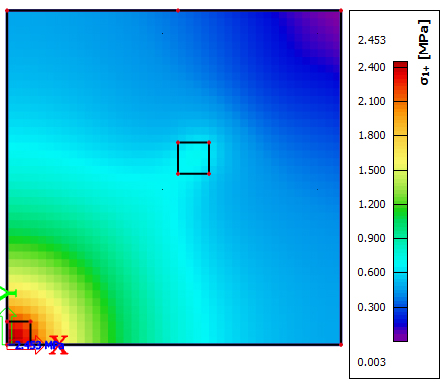
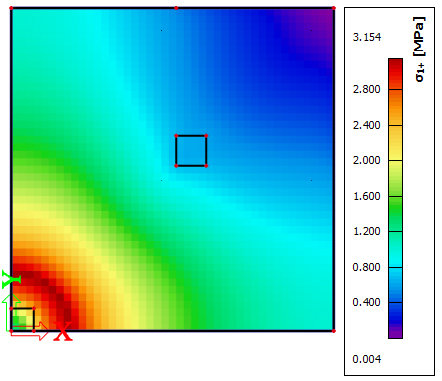
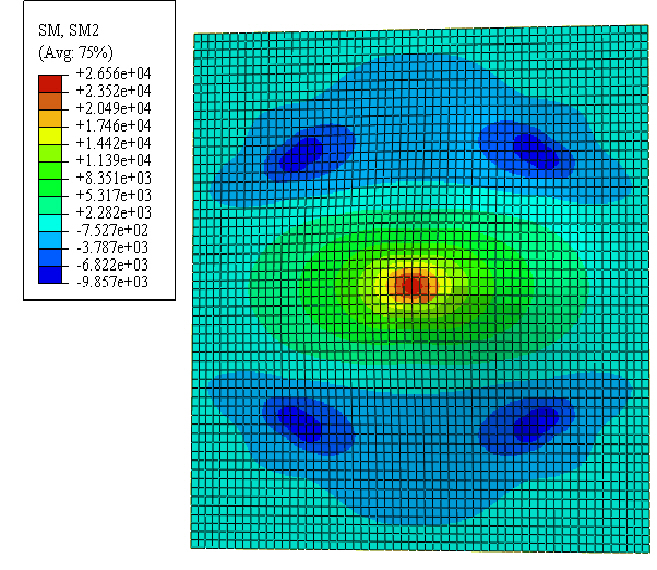
As has been already mentioned, the tight peak in the tension part of the diagram works as a crack localizator. This is perfectly visible in the following figures [Table. 1] where the load is continuously increased. The red colour represents the stress close to the tensile strength and continuous cracking of the slab from the centre of the slab to the edges. The extending middle part to the edges uses just the residual tensile strength of the steel fibre reinforced concrete after cracking. Additionally, these stresses show the places with crack formation in the middle of the slab and theirs spreading of cracks during increasing of the load.
|
F=55,0kN
|
F = 100kN
|
|
F=200kN kN
|
F=283,9kN
|
Table 1. – Principal stress in upper fibres for dosage 30kg/m3
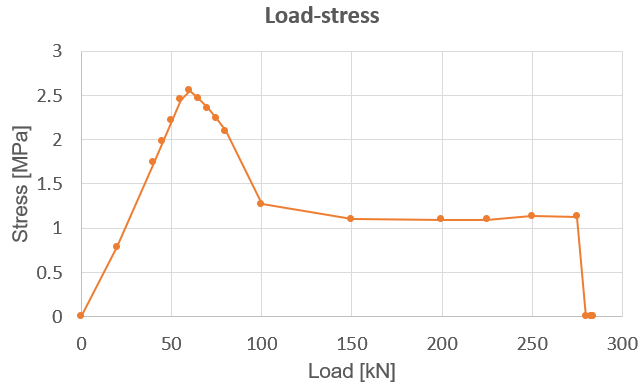
A graph [Fig. 7] can also be made of the dependency between the load level and the stress-strain for the most critical point as in the middle of the slab and upper fibres. When looking at the Load-Stress distribution, it can be deducted that the behaviour of the structure is linear till load level 55kN. The structure is approaching the top of the stress strain diagram peak. A strain very close to 0.1‰ is reached. After that there is a phase of crack formation and the stress is coming down significantly based on the stress-strain diagram. The residual strength in tension (1,09MPa) is reached nearly to load level 100kN corresponding to a strain of 0,3‰. A load higher than 100kN means the spreading of the cracks with smooth hardening of the material done by the increasing branch of the stress-strain diagram in tension till maximal value of 1,13MPa and the plastic load is reached by the load of 283,9kN where the strain reaches the limit of 25‰.
 |
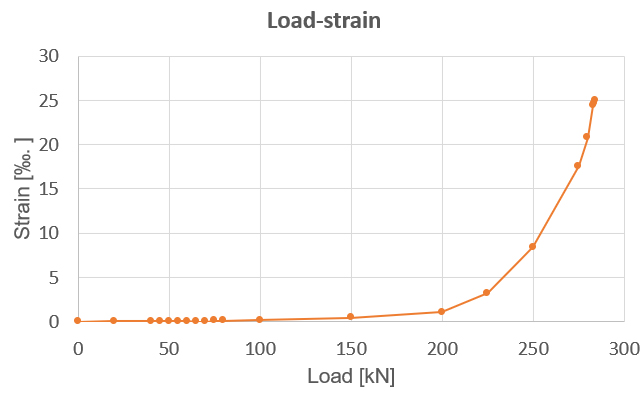 |
Figure 7 a) Load - Stress b) load strain distribution for middle slab point for dosage 30kg/m3
4 Concluding remarks
The experimental and numerical findings presented in the present paper allows to draw the following concluding remarks:
- From test results it turns out that the slabs reinforced only with 30 to 35 kg/m³ of 5D 65/60BG fibers exhibited a good structural behaviour with an extended ductility
- The non-linear calculation performed in software SCIA Engineer provides a very good comparison with the test measurement. The study proves that this tool can be used for the analysis of 2D structures and modelling of the real behaviour of the structure with respect to cracks. A comparison was done for the deflection of two slabs made from C40/50 with fibres DRAMIX 5D 65/60BG and dosage 30kg/m3 and 35kg/m3 respectively. The comparison of the maximal loading capacity mentioned in table [Tab. 2] clearly indicates the higher maximal load is achieved by the test. It means the nonlinear FE calculation provided in SCIA Engineer is on the safe side. The study proves that this tool can be used for the analysis of 2D structures and modelling of the real behaviour of the structure with respect to cracks. The ultimate load capacity in SCIA Engineer was considered as the load where the ultimate tensile strain in the steel fibre reinforced concrete (25‰) is reached and also crushing of the concrete in compression happened.

5 Acknowledgements
The Authors would like to give their appreciation to the Tongji University of Shanghai, China
6 References
[1] ACI Committee 544 (1996), Design considerations for steel Fiber Reinforced Concrete, ACI 544.4R-88, American Concrete Institute, ACI Farmington Hills.
[2] EN 14651-5 (2005). Precast concrete products – test method for metallic fibre concrete – measuring the flexural tensile strength. CEN, p. 20.
[3] Eurocode 2 (2005). Design of Concrete Structures. EN 1992-1-1.
[4] fib, International Federation for Structural Concrete (2012). Model code 2010, Final Complete Draft, Bulletins 65 and 66, March 2012-ISBN 978-2-88394-105-2 and April 2012-ISBN 978-2-88394-106-9.

Want to try SCIA Engineer yourself?
Explore how our software and services can help you optimise your work and boost your productivity. Try it for yourself with a free 30-day software trial.
Download a free 30-days full trial