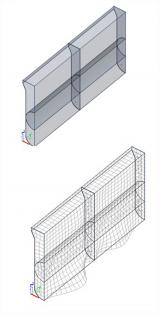
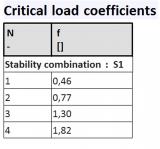
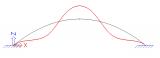
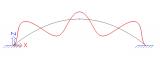
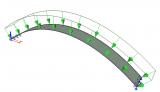
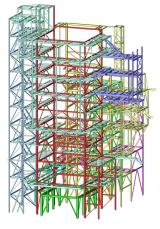
sens.01 - Stability analysis
- Module code sens.01
-
Software
- SCIA Engineer
-
Included in editions
- Concept,
- Professional,
- Expert,
- Ultimate
- Category Analysis & Results
- License Perpetual