Highlights
- Non-linear material behaviour for 2D members
- Can be combined with other non-linearities in SCIA Engineer
- Effective modelling of structures that do not transfer tension, e.g. masonry
- Suitable for complex 3D-structures with shear walls and building cores
- Deep insight in the structural behaviour of structures
This advance module contains friction springs, compression-only surfaces and plastic analysis for beams & surfaces.
Friction springs in nodal supports
Friction supports can be used to model the fact that a reaction component depends on another component. The horizontal component for example depends on the vertical component. When the friction force is surpassed, the support slips through resulting in large deformations.
Friction supports can be used for several types of structures. Almost every support which isn’t rigidly connected to the surface on which it stands is subjected to friction.
Note: Friction can be defined in one or two directions. It is not possible to define friction in all three directions since otherwise the "thrust" cannot be determined. When simple friction (X, Y, Z) is defined in two directions, the option Independent is available. This specifies that the friction in one direction is independent on the friction in the other direction. Composed friction (e.g. YZ or Y+Z) can be specified only in one direction.
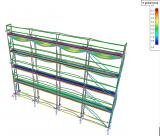
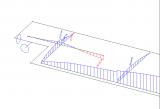
Example of the usage - Scaffolding

Plastic analysis for beams & surfaces
SCIA Engineer implements non-linear material behaviour for 2D members (plates, walls, shells) - plasticity. The plastic zone is based on the isotropic elasto-plastic yield condition (J2 plasticity condition). There is possibility to select from four types of isotropic elasto-plastic materials:
- Von Mises
- Tresca
- Drucker - Prager
- Rankine
Von Mieses and Tresca yield condition
The von Mises yield condition is suitable for ductile materials in general, such as metals (steel, aluminium etc.). It corresponds to a bilinear stress-strain relationship, identical in tension and compression. The plastic branch may have a slope (hardening modulus) or not.
It is a symmetric behaviour, acting in the same way in tension and compression, with or without hardening in the plastic branch.
Tresca yield condition is known also as the maximum shear stress theory. This condition could be also used for metal materials.

Drucker - Prager and Mohr-Coulomb yield condition
Drucker - Prager yield condition is most often used option for concrete where both normal and shear stresses can determine failure. This yield condition can be used for modelling of behaviour of punching, short corbel and for identification of truss analogy to model strut and tie models.


Mohr-Coulomb yield condition is often used to model concrete, soil or granular materials. Condition is similar to the Tresca criterion, with additional provisions for materials with different tensile and compressive yield strengths


Plastic behaviour with other non-linearities
The plastic behaviour of materials may be combined with other types of non-linearity in SCIA Engineer. For instance, plasticity, press only supports and large displacement analysis can be used together. Tension only 1D members with a plastic limit forces may be used to model the behaviour of bolts in a connection.
A typical application of general plasticity is a detailed analysis of non-standard steel connections for which simplified methods do not apply. It may however be applied to any structure that can be modelled using 2D members.
Plasticity is not supported for 1D members. Any beam or truss member that is present in the model is considered as elastic.
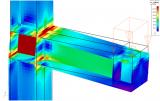



Using general plasticity in SCIA Engineer
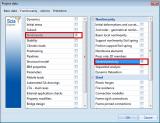
General plasticity is a specific type of non-linearity in SCIA Engineer. After defining the suitable data in the project a non-linear analysis must be carried out to calculate the plastic behaviour of the structure. Please refer to the general information about non-linear analysis in SCIA Engineer. General plasticity is a sub-functionality of non-linear analysis. In the project settings, in the Functionality tab, enable Non-linearity and General plasticity.
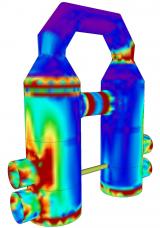
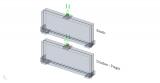
Compression-only surfaces
Analysis of 2D members capable of resisting only compression forces. It can be used e.g. for analysis of masonry walls and arches.

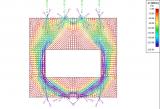
Pressure only finite elements
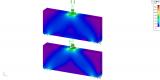
This model gives the user a very good insight into the behaviour of structures such as shear walls or building cores. It is possible to effectively model (reinforced) concrete or masonry structures in a 3D environment. Using a non-linear analysis, the user can reduce all tensile stresses in the concrete or masonry finite elements, which results in a system of compression-only finite elements. The model is capable of displaying the internal arches/struts above openings and doors. Also lintels above openings can be easily modelled and considered in the calculation as hinged beams. Reinforcement in the concrete, capable of resisting the tensile forces, is modelled as an internal rib with the area and stiffness of the reinforcement grade. Using this so-called strut and-tie model the user gets a complete tool to design and check the reinforcement in walls.
A non-linear analysis is performed in order to calculate with the pressure-only finite elements. Using a set of iteration steps the stiffness in the direction of the tension stresses is reduced, thus effectively reducing the tensile stresses in the structure. If the geometry of the structure is such that a new state of equilibrium in ultimate limit state is found, i.e. by internal arches or reinforcement, the convergence criterion will be reached.
Using the function for displaying the trajectories of the principal forces or stresses the user is able to adequately review the behaviour of the structure. The internal struts and ties can be clearly seen. The internal forces on the reinforcement can be displayed as axial forces in the structure. Other results like reactions and deformations also help the user to get the proper insight into the behaviour of the structure.
This module helps the engineer in the design and checking of complex 3D-structures with shear walls and building cores. A practical example shows the difference between a linear elastic analysis (according to the service limit state) and a non-linear analysis using pressure only finite elements (according to the ultimate limit state).
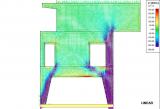
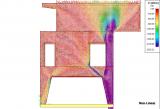
The pressure only finite 2D-elements is a must have add-on for the engineer who calculates 3D-structures or 2D-walls in day-to-day practice. This module supplies an adequate insight into the structural behaviour of the structure. Using this module the user can effectively model masonry or reinforced concrete structures. Practical applications can be masonry walls with openings, concrete walls with openings, special concrete details like tooth-supports of beams.
Required modules:
- sen.00

Want to try SCIA Engineer yourself?
Explore how our software and services can help you optimise your work and boost your productivity. Try it for yourself with a free 30-day software trial.
Download a free 30-days full trial