Calculate center of gravity (mass)
The only possibility to calculate the center of gravity is by means of the resultant of reactions & the position of the central point.
Then the resultant internal forces can be calculated back to find the center of gravity.
STEP 1: create 3 load cases
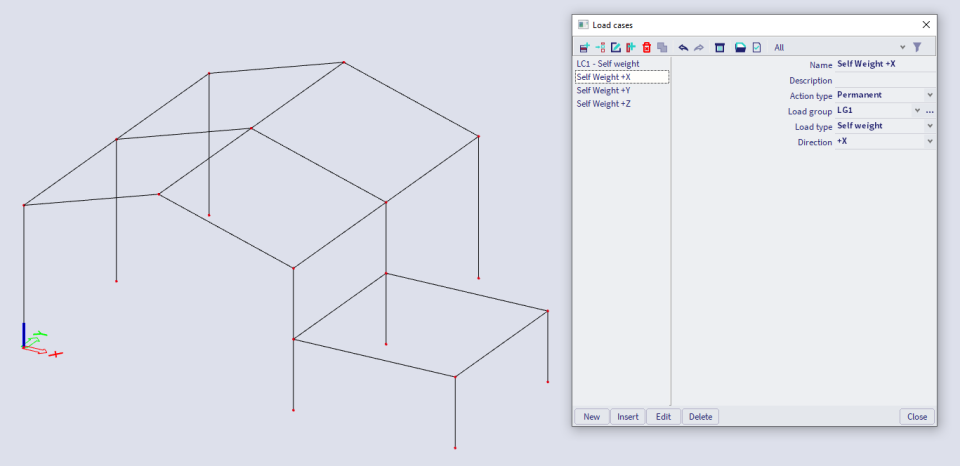
Create 3 load cases: 'Self Weight +X', 'Self Weight +Y' and 'Self Weight +Z'. The figure below shows the settings for load case 'Self Weight +X'. The other load cases are set similarly.
STEP 2: calculation
Execute the linear calculation.
STEP 3: results
Look at the result 'Resultant of reactions' (Main menu > Results > Supports) for the 3 created load cases.
The figure below shows the result for load case 'Self Weight +X'
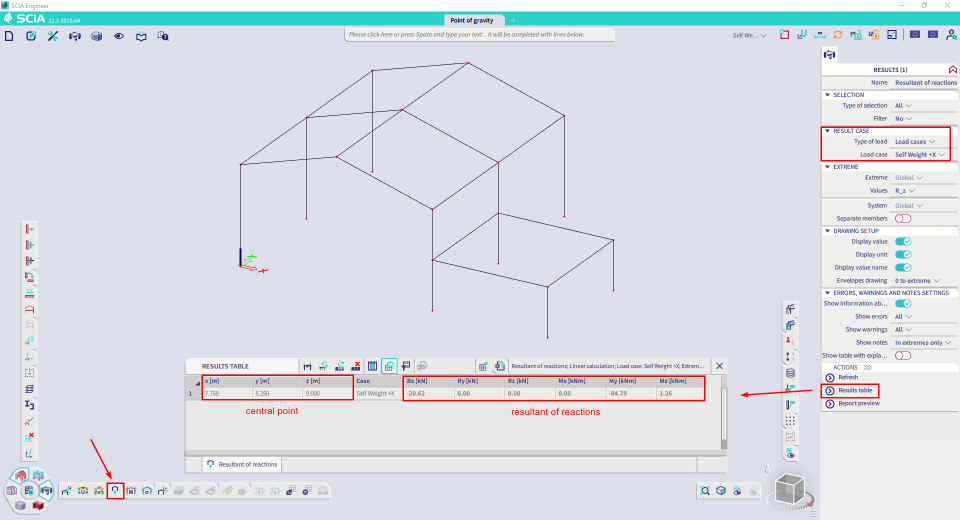
You also need the central point. The coordinates of this point can be found as well in the results table (if this is not visible, you can right-click in the bar and choose for 'Add all columns').
You can copy these results from the results table immediately to MS Excel.
STEP 4: calculate the center of gravity
The equations for a 3D structure in the center of gravity are:
- Mx = Rz*dY - Ry*dZ
- My = Rx*dZ - Rz*dX
- Mz = Ry*dX - Rx*dY
For load case 'Self Weight +X' (Ry and Rz are 0) this becomes:
- My = Rx*dZ => dZ = My/Rx
- Mz = -Rx*dY => dY = -Mz/Rx
For 'Self Weight +Y' (Rx and Rz are 0) this becomes:
- Mx = -Ry*dZ => dZ = -Mx/Ry
- Mz = Ry*dX => dX = Mz/Ry
For 'Self Weight +Z' (Rx and Ry are 0) this becomes:
- Mx = Rz*dY => dY = Mx/Rz
- My = -Rz*dX => dX = -My/Rz
Calculate the center of gravity (Xc, Yc, Zc) with:
- Xc = X + dX;
- Yc = Y + dY
- Zc = Z + dZ
(X, Y, Z) are the coordinates of the central point.
Following Excel-file calculates the point of gravity automatically with the formulas that are described above: