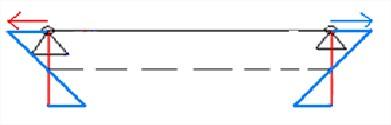
Influence of an eccentricity on internal forces
By entering an eccentricity the system line (full) doesn’t coincide with the reference line (aborted) anymore. The reference line shows the centre of gravity of the cross-section. However, the system line is important to the program, because the system lines determine whether the entities are connected to each other or not. Moreover the supports are also introduced on the system line.
TIP: Reference line can be activated via View parameters settings > Structure > Structure > Member system line
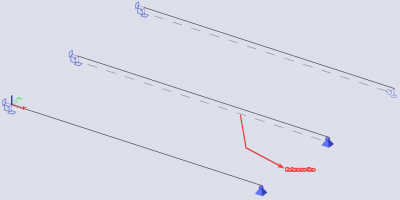
In the example below a comparing study of 3 situations is made. In every situation a beam of 10 m, supported on both ends by hinged supports, to which a load of 10 kN/m is applied, is regarded.
- The first beam is the standard situation without eccentricity.
- The second beam has an eccentricity ez of -200 mm and the displacement in the longitudinal direction is fixed.
- The third beam has an eccentricity ez of -200 mm but the displacement in the longitudinal direction is free.
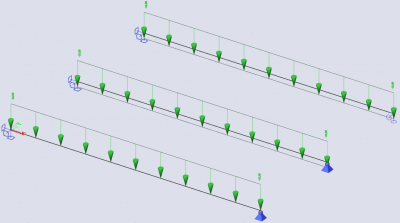
The first beam shows a resulting normal force equal to zero. This is logic since exterior normal forces are nowhere applied.
The second beam, however, has a resulting tensile force in the beam that differs from zero. This resulting tensile force does not occur in the third beam where the displacement in the longitudinal direction is free.
The supports are introduced on the level of the system line and not on the level of the neutral vessel. Because of this a normal force is working in a resulting way on the neutral vessel because the support can take an axial reaction force. The resultant of these reaction forces is zero because no exterior axial force occurs.
Resulting works a tensile force on the beam. The resultant of the reaction forces is zero.