Automatic calculation of effective width
Choosing an appropriate model is key when performing the structural design of beams. One important factor to be considered is the effective width calculation when considering a T-section and this depends on the slab and beam dimensions, the type of loading, the span, the support conditions, and the transverse reinforcement.
In SCIA Engineer the calculation of the effective width is done automatically based on the EN1992-1-1 clause 5.3.2.1:
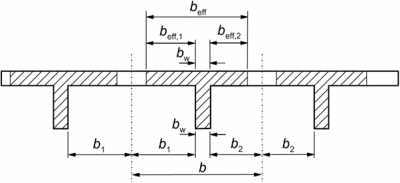
beff = ∑beff,i + bw < b
where: beff,i = 0,2 bi + 0,1l0 < 0,2 l0 and beff,i ≤ bi
l0 is the effective span length, or distance between the point of zero-moment in the considered span:

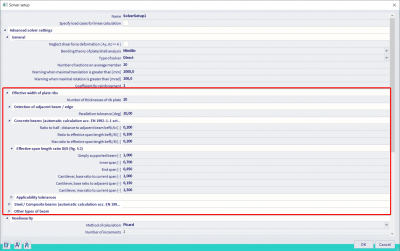
All the above factors can be modified in SCIA Engineer in the solver settings:
To determine the contact width between the rib and the slab the placement of the beam is used:
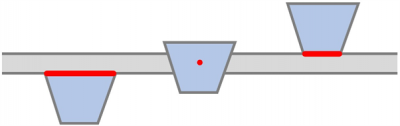
- Bottom, then the upper face of the cross-section is considered
- Centre, then the contact width is taken as zero; please note, that this is a case where the formulas from the Eurocode do not apply, as the resulting cross-section cannot be considered as a T-section.
- Top, then the lower face of the cross-section is considered
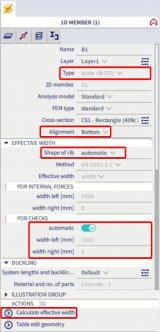
To be able to use the automatic effective width calculation in SCIA Engineer you need the following:
- The 1D element needs to be of type: Rib
- Alignment of the beam needs to be either top or bottom
- The shape of the rib needs to be on automatic
- The automatic calculation for checks needs also to be ticked in order to use the values from the EN1992, if unticked the user has to manually define the width to be used for checks.
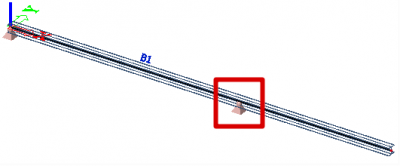
Keep in mind that the span length does not necessarily correspond to the length of the 1D member, this is something that a user needs to know if the automatic width of the calculation is to be used. For example, in the picture below we can see that we have two spans but modelled as 1 straight beam:
To have the correct calculation of the effective width user needs to split the beam in two:

The same applies when we have a difference in the width at one side of the beam like the example below:
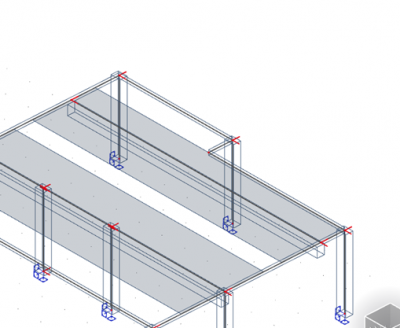
The user needs to split the beam to have the effective width calculated correctly: